The Basics

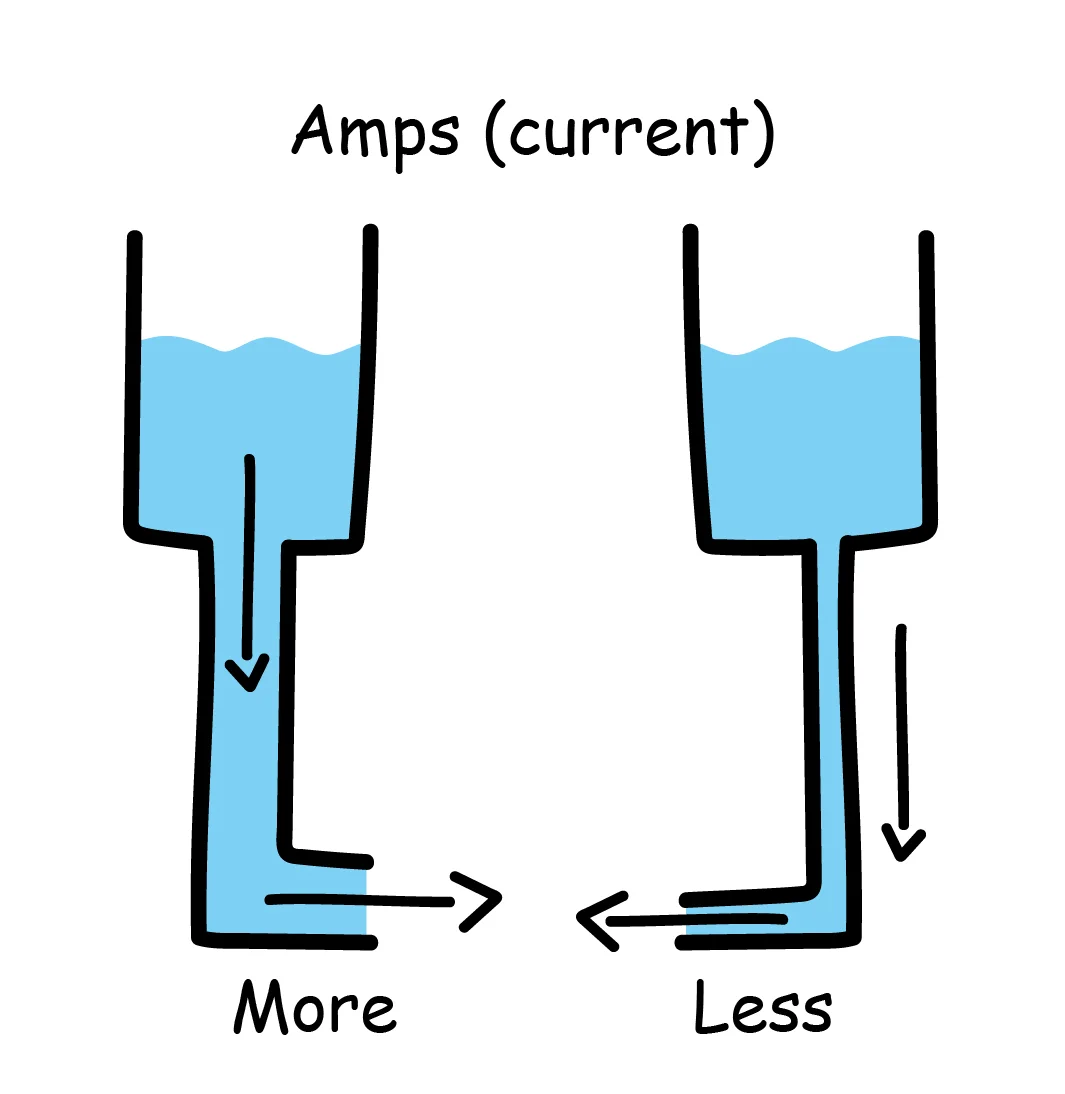
Let’s start with the basics. Electrical current is measured in amps (A), and represents the flow of negatively charged electrons. The simplest depiction of electrical current is water flowing through a pipe. Amps are analogous to a rate of movement in classical mechanics. 

Voltage, on the other hand, which is measured in volts (V), is the amount of energy in each unit of electrical charge. In the pipe metaphor, voltage is like the water pressure. In terms of classical mechanics, voltage is analogous to work, or how much energy it takes to lift something up against gravity. 

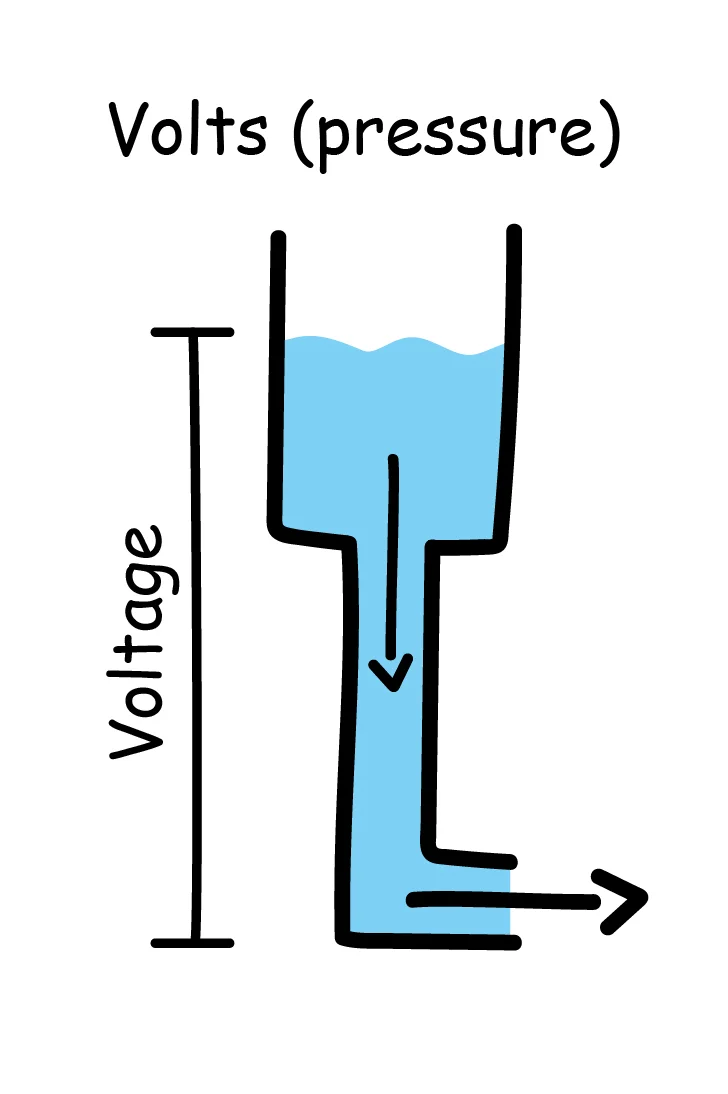
So, volts are a measure of the electricity’s strength, and amps are the volume of flowing water. If there is more water pressure flowing through the pipes, the speed of the water flowing through the pipes is higher. Similarly, the electrical current flowing through a circuit depends on the voltage.

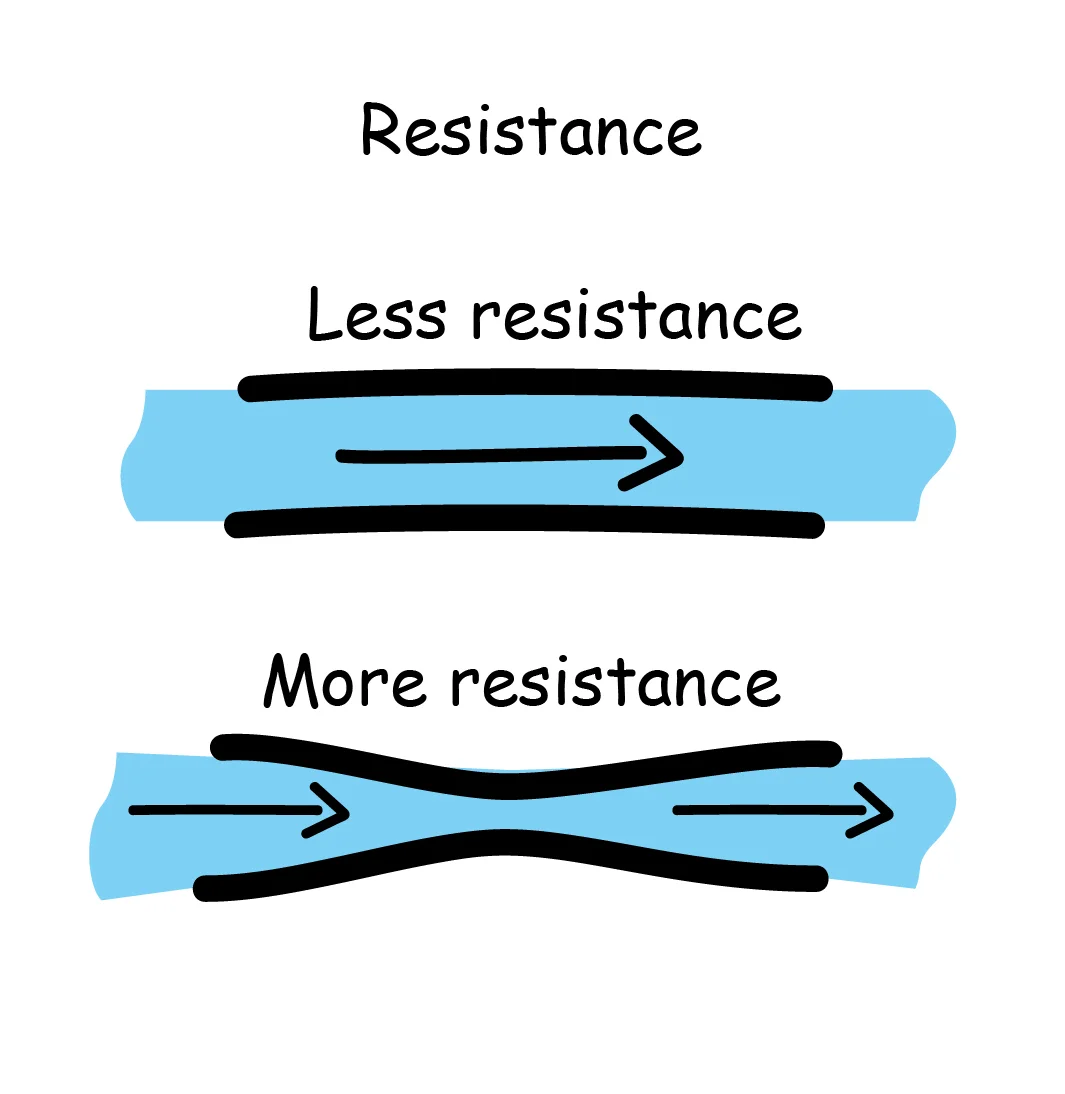
One final building block is required to understand the basics of electronics - resistance. Resistance, measured in ohms, is exactly what it sounds like - a material’s tendency to resist the flow of charge. Coming back to the pipe analogy, the resistance is related to the width of the pipe. Cinching the pipe in the middle will create a narrow section, therefore increasing resistance as the pipe “resists” the flow of water (or electricity, in the case of flowing electrons). 

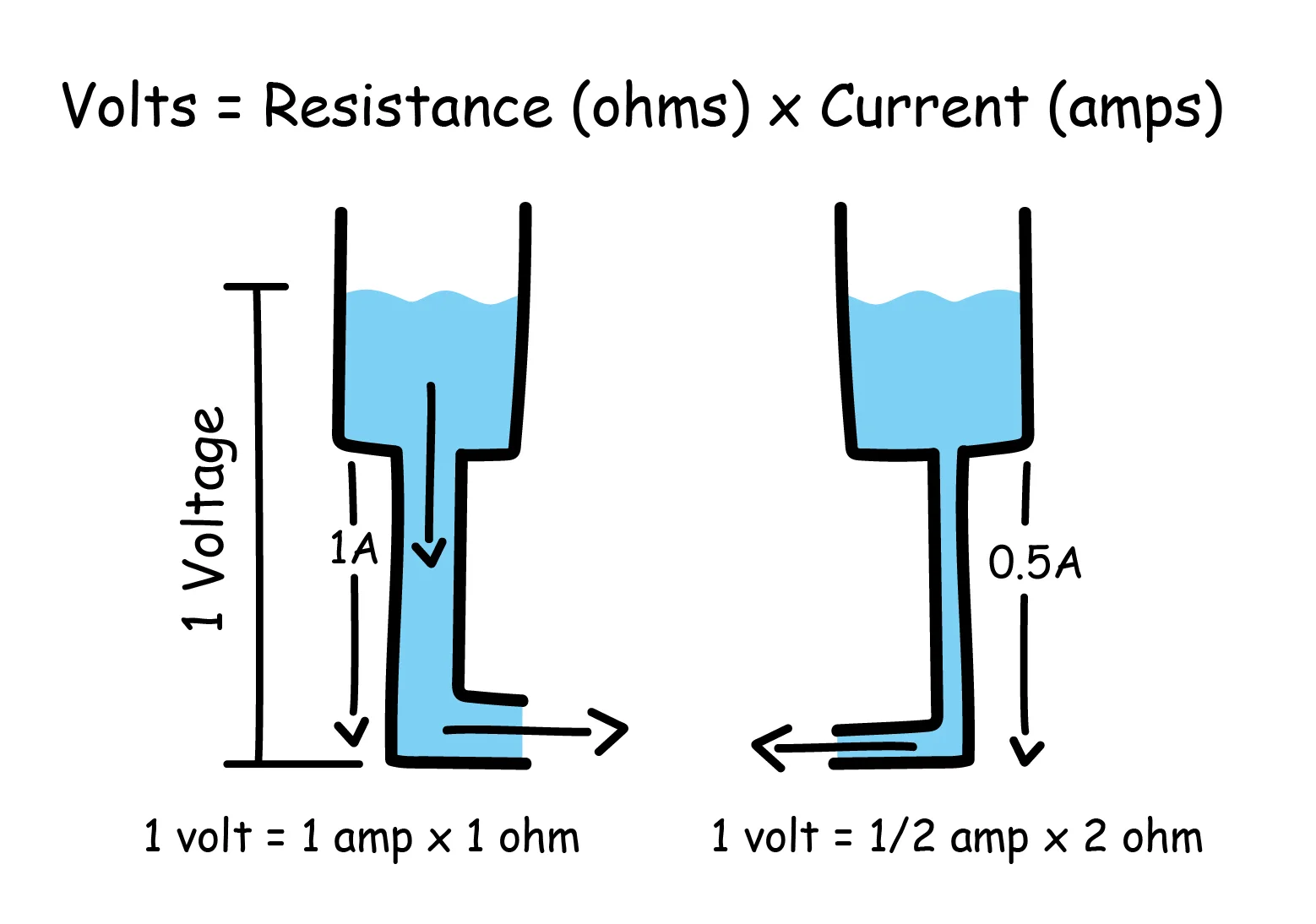
Ohm's law connects the three variables with a simple mathematical equation: V = I x R (where I = current and R = resistance). This law shows that the voltage difference between two points is proportional to the electric current flowing between them, and to the resistance the current will experience.

When we talk about consumable electronics, we often have information for both the voltage and current. Using another simple relationship, we can determine charging rates.

How does this translate to charge rate?

To determine charging rate, we need to figure out the rate that energy can be transferred to the battery. In other words, we need to find the power, which measures how much work can be performed in a given amount of time. Power is a measure of how rapidly the work is done and is measured in kilowatts. Since voltage is a type of work and amperage is a rate, we can connect these concepts with the following equation: 

Power(kW) = V(volts) x I(amps)

‍

Here’s a quick example from classical mechanics to help this make sense. 

One of my favorite activities is hiking. Mount Shasta is a well-known area in Northern California for challenging hikes. Hiking the popular Avalanche Gulch Route is a brutal 10.1 mile hike that covers 7300+ feet of elevation gain. Several additional mountaineering routes exist that cover the same elevation gain but areas with much steeper grades, covering the 7300+ feet over a shorter distance. One such route on the northeast face of the mountain covers the same 7300 feet in only 8.5 miles. In terms of vertical gain, both routes result in reaching the same summit. Since work against gravity only depends on how high you’re going, these two routes take the same amount of work. However, although the ultimate height reached is identical, the time it takes to get to the top is not. The steeper, mountaineering route will take much longer. 

The Avalanche Gulch Route typically takes a good hiker 8 hours to complete - a rate of 912 feet/hour. The shorter mountaineering route, on the other hand, typically takes around 10 hours, at a lower rate of only 730 feet/hour. Given that the pure hiking route brings you to the same height in considerably less time, a hiker’s rate of ascent, or power, is higher. In this example, the vertical distance covered is like the voltage (7300 feet), and the pace is like current (feet/hour).

Hopefully this gives you a decent sense of how volts and amps relate to something physical you can think of. Now, we can look at a few examples of how this works with EV charging.

Level 1 (L1)

Most homes in the U.S. are equipped with a combination of 15-amp and 20-amp, 120-volt circuits. Charging via a 120V circuit is considered Level 1 charging. Using the Chevrolet Bolt EV as an example, we can choose to charge at 8A or 12A depending on what circuit we are using. 

Note that circuit breakers can only handle about 80% of their overall amperage, so you will never be able to use the full amps that your circuit has. 

• P = V x I = 120V x 8A = 960W = 0.96 kW
• P = V x I = 120V x 12A = 1440W = 1.44 kW

We can then use this information to determine how long it will take to charge the car based on specified power. These numbers will also be influenced by charging efficiency, as not all of the generated electricity will be delivered to the battery (losses). But, let’s pretend that our charger has nearly perfect efficiency. 

• Time (8A) = battery size ÷ charge rate = 65 kWh ÷ 0.96 kW = 67.7 hours
• Time (12A) = battery size ÷ charge rate = 65 kWh ÷ 1.44 kW = 45.1 hours

Level 2 (L2)

Circling back to the power equation, we can increase the charge rate by increasing the voltage or increasing the current. To charge with adequate speed and safety, higher voltage outlets are essential. Why can’t we increase the current, instead?

1. High current requires large conductors, which are materially intensive (increasing costs)
2. Protective systems such as circuit breakers are designed for a specific current. If you wanted to use a higher current, the circuit breakers would need to be larger, more difficult to install, and more expensive.
3. Charging losses are proportional to the current squared, so you would lose a lot more electricity to waste heat if you increase current (e.g. doubling the current increases heat losses by four)

L2 chargers typically operate between 208-250V and a maximum current of 80A, yielding a maximum power output of 19.2 kW. 

Standard outlet = 240V

Maximum current = 100A breaker -> 80A (since circuit breakers can only handle about 80% of their overall amperage)

• P = 240V x 80A = 19.2 kW

If you think back to our article on different charging rates, you might remember that L2 charging requires use of the onboard charger that is built into the car. Onboard chargers typically range from 3.3 kW to 22 kW. The new Chevrolet Bolt EV, for example, comes with an 11.5-kW onboard charger, meaning that it cannot achieve the maximum L2 rate of 19.2 kW. In fact, the only EVs on the market that can maximum the L2 power are some variants of the Tesla Model S and Audi e-trons. 

Level 3 (L3)

L3 charging, or DC fast charging, requires inputs of at least 480V and 100A, yielding a minimum power of 48 kW. Some of the early EVs, such as the Chevrolet Bolt EV, are only capable of 48A level 2 charging and 150A level 3 charging. 150A charging yields a charge rate of roughly 55kW, far below what many new chargers are capable of producing. Tesla V3 superchargers, for example, are capable of 250kW. Similarly, many EVgo chargers are capable of 350kW, despite very few vehicles being capable of handling such loads. 

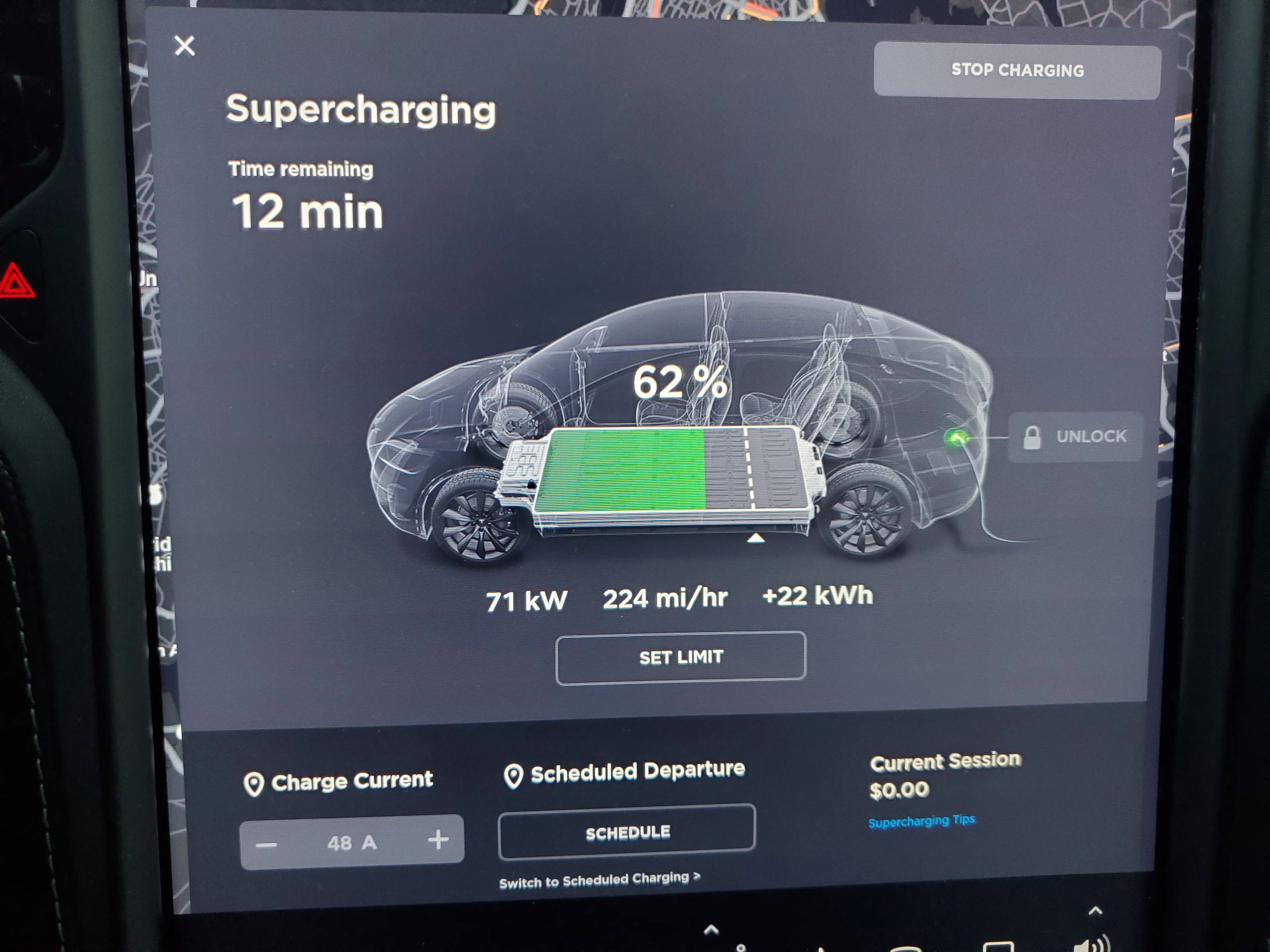
When choosing a charging speed, several considerations are required:

1. Limits of the EV - choosing a higher-powered fast charger over a lower-powered one does not guarantee that you’ll charge more quickly. You can usually google the maximum charge power. For the Bolt, with its max charging speed of 55 kW, the peak charging rate would be approximately the same whether you stopped at a charger rated at 62.5 kW, 150 kW or 350 kW‍
2. ‍Charge time - we generally suggest saving fast charging for road trips and special situations, especially if you have access and time to use level 2 charging. Although cars have a lot of hardware and software to keep batteries safe from fast charging, it is still unknown how much an impact it may have on long term battery life. 

Voltage or Current - Who is in Control?

Generally speaking, charging stations with higher voltage can deliver more power, which often leads to faster charging times when compared to chargers with lower voltage and higher current. As previously mentioned, high voltage (rather than high current) helps to minimize the energy losses associated with resistance in the charging cables. This improves the efficiency of charging, ensuring less energy is lost as heat and more is delivered to the battery. It also may help prevent the battery and charging equipment from getting as hot as it would with a higher amperage system. To this end, many new ultra-fast chargers are rated for 1000V, which allows lower currents to be used to achieve the same power output. 

Other Factors that Influence Charge Rate

In addition to choosing a charge rate based on choosing a specific charger, many other factors contribute to charging speeds. 

1. Ambient temperature - extreme temperatures significantly reduce charge speeds
2. Battery temperature - ensuring the battery is at an ideal temperature (pre-conditioning) is important for reaching maximum charge rates
3. Heat - high temperatures result in additional battery cooling needs, reducing the energy going into the battery
4. Cold - low temperatures result in slower moving molecules, making it more difficult to add energy to the battery
5. State of charge - batteries can only charge at maximum rate for part of a charging session, usually in the lower half of the battery pack, but depends on the battery and the internal management system. One constant across all charging curves is a significant ramp down of charging speed at approximately 80% charge, a protective mechanism for lithium-ion batteries.
6. Charge curve - depending on the internal battery management system and battery composition, each vehicle has a unique charge curve as the state of charge increases.

A Note on C-rate

C-rate is another term that may come up if you’re diving into volts, amps, and power. C-rate is a measure of the rate at which a battery is charged or discharged relative to its capacity. 1C is defined as the power that would, over an hour, charge or discharge the complete capacity of a battery at 1 amp. For the Chevrolet Bolt EV, which has a ~65 kWh battery, 1C is 65 kW. For the same car, 2C would be 130 kW (charge or discharge in half an hour), and 0.5C would be 32.5 kW (two hours to charge or discharge the battery). It’s important to note that C rate does not mean that a battery can be fully charged or discharged at this constant power; it is simply a ratio of power to battery capacity. 

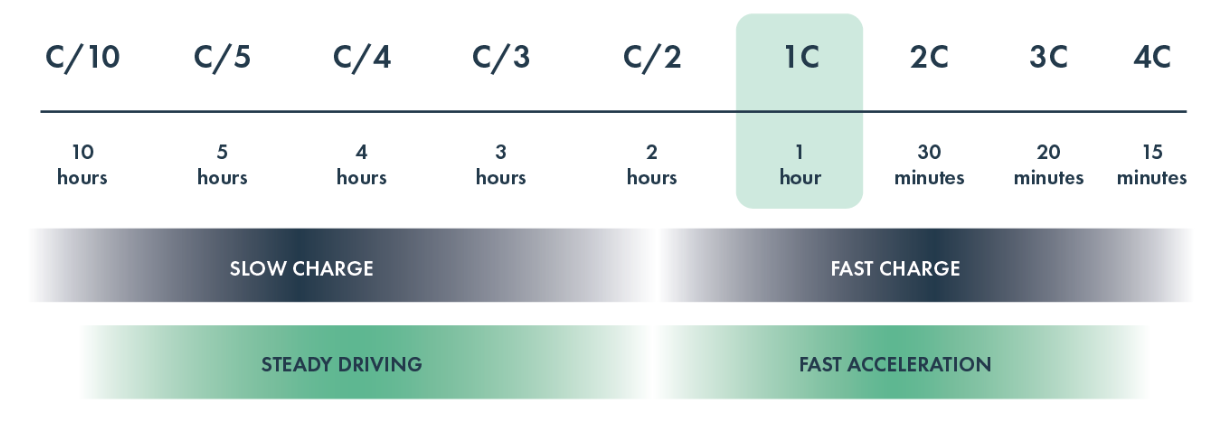
In an ideal world, a battery would perform at extremely high C-rates all the time. However, generally speaking, higher C-rates make it more difficult for a battery to deliver reliable performance and increase the risk of battery degradation. EV battery chargers do not sustain charging rates higher than 2C for longer than a few minutes before the charging rate is reduced to avoid causing damage to the battery. In some cases, such as the Chevrolet Bolt EV, the max charging rate is below 1C, likely the result of a first-generation battery management system and rigid protocols to protect the battery health.